In this post, we will talk about the multiple linear
regression using Excel. We will learn about the basic assumptions of classical
linear regression model, performing regression using Excel, and interpreting
the result.
Let’s start with the basic definition of regression analysis.
The term regression was introduced by Francis Galton in
their research paper. Modern interpretation of Regression analysis is concerned
with the study of dependence of one variable (dependent variable), on one or
more other variables (the explanatory or independent variables), with a view of
estimating or predicting the dependent variable’s value in terms of independent
variables.
Method of estimation:
There are two mostly used method of estimation
1-
Ordinary Least Squares (OLS)
2-
Maximum Likelihood (ML)
OLS is highly used method for estimation because it is
intuitive appealing and simpler than ML method. Besides, in linear regression
context the both methods generally give similar results.
Assumptions of OLS
method:
These are the following assumptions of OLS. Under these
assumptions, OLS has some useful statistical properties which makes it one of
the most powerful method of regression analysis. Regression model will be valid
under the following assumptions.
1-
Regression model is linear in parameters, though it may or may not be linear in the
variables i.e. regressand Y and regressor X may be nonlinear.
Yi = β0 + β1 Xi + ui
2-
Fixed regressor X or X values are independent of
the error term
i.e. covariance(Xi ,ui)
= 0
3-
Expected value or mean of error term (random
disturbance) is zero.
E(ui) = 0
4-
Variance of error term (random disturbance) is
same regardless of the value of regressor X. This property is called Homoscedasticity (Home – equal ,
Scedasticity – spread i.e. equal variance)
Var(ui) = σ2
Homoscedasticity refers to the assumption that that the dependent
variable exhibits similar amounts of
variance across the range of values for an independent variable.
Heteroscedasticity is the absence of homoscedasticity.
5-
No
Autocorrelation between the any 2 error terms (random disturbances).
covariance(ui
,uj) = 0 i ≠
j
6-
No Multicollinearity
between the any 2 regressors or X values.
covariance(Xi ,Xj) = 0 i ≠ j
7-
Number of observations must be greater than number
of parameters to be estimated.
For example, we have the data set for a store who sells cold
drinks. We need to find out the relation between the demand of cold drink (dependent variable) and the price of cold drink & advertisement expenses done
(independent variable).
Week
|
Demand (Q)
|
Price (P)
|
Ad
Expenses (A)
|
1
|
51345
|
2.78
|
4280
|
2
|
50337
|
2.35
|
3875
|
3
|
86732
|
3.22
|
12360
|
4
|
118117
|
1.85
|
19250
|
5
|
48024
|
2.65
|
6450
|
6
|
97375
|
2.95
|
8750
|
7
|
75751
|
2.86
|
9600
|
8
|
78797
|
3.35
|
9600
|
9
|
59856
|
3.45
|
9600
|
10
|
23696
|
3.25
|
6250
|
11
|
61385
|
3.21
|
4780
|
12
|
63750
|
3.02
|
6770
|
13
|
60996
|
3.16
|
6325
|
14
|
84276
|
2.95
|
9655
|
15
|
54222
|
2.65
|
10450
|
16
|
58131
|
3.24
|
9750
|
17
|
55398
|
3.55
|
11500
|
18
|
69943
|
3.75
|
8975
|
19
|
79785
|
3.85
|
8975
|
20
|
38892
|
3.76
|
6755
|
21
|
43240
|
3.65
|
5500
|
22
|
52078
|
3.58
|
4365
|
23
|
11321
|
3.78
|
9525
|
24
|
73113
|
3.75
|
18600
|
25
|
79988
|
3.22
|
14450
|
26
|
98311
|
3.42
|
15500
|
27
|
78953
|
2.27
|
21225
|
28
|
52875
|
3.78
|
7580
|
29
|
81263
|
3.95
|
4175
|
30
|
67260
|
3.52
|
4365
|
31
|
83323
|
3.45
|
12250
|
32
|
68322
|
3.92
|
11850
|
33
|
71925
|
4.05
|
14360
|
34
|
29372
|
4.01
|
9540
|
35
|
21710
|
3.68
|
7250
|
36
|
37833
|
3.62
|
4280
|
37
|
41154
|
3.57
|
13800
|
38
|
50925
|
3.65
|
15300
|
39
|
57657
|
3.89
|
5250
|
40
|
52036
|
3.86
|
7650
|
41
|
58677
|
3.95
|
6650
|
42
|
73902
|
3.91
|
9850
|
43
|
55327
|
3.88
|
8350
|
44
|
16262
|
4.12
|
10250
|
45
|
38348
|
3.94
|
16450
|
46
|
29810
|
4.15
|
13200
|
47
|
69613
|
4.12
|
14600
|
48
|
45822
|
4.16
|
13250
|
49
|
43207
|
4
|
18450
|
50
|
81998
|
3.93
|
16500
|
51
|
46756
|
3.89
|
6500
|
52
|
34593
|
3.83
|
5650
|
Performing multiple
regression in Excel
1-
Click on the data tab. Then click on the menu Data Analysis at the corner. Then a pop up window will open. Now
select Regression from this pop up
window. And click in OK.

2-
Now a pop up window will open asking for inputs.
Now click on arrow sign to select the X range (Regressor) and Y range.

3-
You can select any of the parameters like
confidence interval (by default it is 95%) or any other as per your requirement.

4-
Now select the output range. You have options to
get output in same work sheet, new worksheet and new workbook. Here we want to
get output in same worksheet and selected a range. As you can see in above pic.
Now press OK to get output.
Interpretation of
regression output:
Regression Statistics
table:
Multiple R – is the
coefficient of multiple correlation. You may be knowing the bivariate
correlation. Multiple correlation can be interpreted in the same way. R is a measure of the strength of the association
between the independent variables and the one dependent variable.
R Square – is the
square of Multiple R. It is called as multiple coefficient of determination. It is useful to explain that how much
of total variation can be explained by the predicted model. It is measure of
goodness of fit of predicted model.
In our case R square = 0.263782. It means that 26.37% of the
variation (variation of Y around its mean) can be explained by the model (by
independent variables).
Unfortunately, in case of multiple regression R square is
not the unbiased estimation of coefficient of determination. Adjusted R square is
a better estimate for coefficient of determination in case of multiple
regression.
Adjusted R Square -
It indicates that how much of total variation can be explained by the model,
adjusted for the degree of freedom. It should be used in place of R square for
multiple regression
Where k = the number of variables in the
model (Independent as well as dependent) and n = the number of data elements in the
sample.
In our case, k=3 (2 IV, and
1DV) , and n =52
Standard Error - refers to the estimated
standard deviation of the error term u. Sometimes it is called as standard
error of the regression.
Standard
Error = sqrt(Square sum of error ∕(n-k))
ANOVA Table:
Sum Squares (SS) corresponding to regression is called Explained Sum Square (ESS) or Sum
Square Regression (SSR).
Sum Squares (SS) corresponding to residual is called Residual Sum Square (RSS) or Sum
Square Error (SSE).
Total Sum Square (TSS) = ESS + RSS
Mean Sum Square = SS/df
Significance of F – indicates weather value of R square is significant or not i.e. significance
of measure of goodness of fit.
Coefficients - gives the least squares estimates of βj.
Standard
error- gives the
standard errors of the least squares estimates bj of βj.
t Stat- gives the
computed t-statistic for hypotheses H0: βj = 0 against Ha: βj ≠
0. It checks for the significance of the parameter βj values. Also
called as significance test.
T stat = Coefficients / Standard error.
It is compared to a t value from t-table with df degrees of freedom and a
particular confidence interval (1-α).
P-value- gives the p-value for test of H0: βj =
0 against Ha: βj ≠ 0. It is the testing of hypotheses.
As we have taken a confidence interval of 95%. So, if p-value corresponding to a parameter is less
than 0.05. Then, we will reject the Null Hypothesis i.e. βj ≠ 0
or is significant.
Note that this p-value is for a
two-sided test. For a one-sided test divide this p-value by 2 (also checking
the sign of the t-Stat).
Columns Lower 95% and Upper 95% values define a 95% confidence interval for βj.
Estimated Regression Model:
Estimated Industry Demand (Q
cap) = 100626.034 -16392.63 * Price (P) + 1.5763295 * Ad Expense (A)




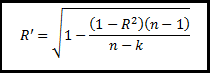

No comments:
Post a Comment